3.1. MEDIDA DE LOS RESULTADOS EN UNIDADES FÍSICAS/CLÍNICAS
La tradición biomédica ha basado la medición del estado de salud o CVRS de los pacientes en criterios objetivos sustentados en la observación clínica. Las pruebas de laboratorio, los procedimientos diagnósticos o la propia exploración clínica ofrecen mediciones cuantificables en unidades físicas/clínicas, que pueden aplicarse para evaluar la efectividad de los programas sanitarios. No obstante, tales evaluaciones sólo tendrán sentido si el efecto de los programas que se comparan puede reducirse a una única e idéntica dimensión. Dicha dimensión suele consistir en una característica bioquímica (por ejemplo, saturación de oxígeno de la hemoglobina), fisiológica (por ejemplo, carga viral), anatómica (por ejemplo, ángulo de giro de la rodilla), funcional (por ejemplo, capacidad para caminar sin ayuda) o relacionada con la supervivencia o la longevidad.
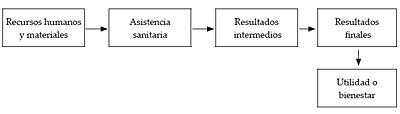
Aunque la medida concreta que se utilice dependerá del tipo de intervención sanitaria a evaluar, en general, resultará más congruente con los fundamentos de la evaluación económica escoger aquellas unidades que tienen un impacto más directo en el bienestar de las personas. Para entender lo que queremos decir, resulta útil pensar en la atención sanitaria, sus resultados y el bienestar derivado como los elementos de una función de producción de salud.
Como puede verse en la figura 2 la asistencia sanitaria produce unos primeros resultados relacionados con la salud que hemos calificado de intermedios. Un resultado intermedio sería la reducción del nivel de colesterol de un paciente. A su vez, cabe suponer que el mantenimiento de niveles reducidos de colesterol reducirá el riesgo de sufrir una enfermedad coronaria, incrementando así la esperanza de vida. Esta mayor longevidad sería un ejemplo de lo que en la figura hemos denominado resultados finales.
Figura 2. La función de producción de la salud
Esto no significa que las medidas clínicas basadas en variaciones bioquímicas o fisiológicas no sean importantes –lo son y mucho para los médicos– pero poseen un interés limitado para los pacientes y la población general, no existiendo siempre una correlación estrecha entre cuantificación objetiva de la salud y nivel de bienestar. Por tanto, entre la utilización de una medida de efectividad de resultados intermedios como el porcentaje de reducción del colesterol y una medida de efectividad de resultados finales como los años de vida ganados, preferiremos esta última. Otros ejemplos de medidas de resultados finales serían los casos de insuficiencia venosa detectados, los días libres de episodios asmáticos, o las muertes evitadas.
Las medidas de efectividad pueden provenir de dos fuentes distintas 10: los ensayos clínicos controlados y los estudios observacionales. Las implicaciones que encierra escoger entre una u otra fuente han sido caracterizadas por Rittenhouse y O’Brien (1996) como un intercambio (tradeoff) entre validez interna y validez externa. Por un lado, los ensayos clínicos poseen una gran validez interna, debido a que resulta improbable que las diferencias detectadas entre los grupos de tratamiento estén sesgadas, ya que los sujetos han sido asignados aleatoriamente a cada uno de los grupos. Sin embargo, los ensayos pueden tener escasa validez externa, ya que suelen desarrollarse en condiciones ideales, muy distantes de la práctica clínica real (por ejemplo, criterios estrictos de inclusión/exclusión). Por el contrario, los estudios observacionales reflejan las condiciones en que se desarrolla la práctica médica real, pero debido a la ausencia de comparaciones controladas resulta arriesgado extraer conclusiones causa-efecto.
Ante la anterior disyuntiva, se han formulado (Drummond, 1998) dos posibles soluciones. La solución más costosa consistiría en realizar ensayos clínicos con un diseño más pragmático. Estos ensayos serían aleatorios como los ensayos tradicionales de corte experimental, pero se aproximarían más a la práctica clínica normal, evitando, por ejemplo, la aplicación de protocolos atípicos para la administración de los procedimientos terapéuticos. Sin embargo, ante lo costoso de la implementación de este tipo de ensayos pragmáticos –en términos de tamaño muestral, por ejemplo– se impone la necesidad de alcanzar un equilibrio entre calidad de los datos y relevancia de los mismos para la evaluación económica. Esto se consigue mediante la modelización, en la cual se integran los datos experimentales provenientes de los ensayos controlados una vez corregidos o ajustados para responder en mayor medida a las condiciones efectivas en que se ejerce la práctica clínica. Por ejemplo, O’Brien et al., (1994) en un ACE de dos tratamientos profilácticos para la trombosis venosa aguda tras el reemplazamiento de cadera, ajustaron a la baja las tasas de trombosis detectadas en los ensayos clínicos para recoger el hecho de que muchas de esas trombosis eran poco importantes desde el punto de vista clínico. Esto se debe a que el protocolo del ensayo implicaba la realización de venografías sistemáticas, detectando trombosis asintomáticas que en la práctica clínica regular no habrían sido percibidas ni por el paciente ni por el médico. De hecho, como puso de manifiesto el meta-análisis realizado por O’Brien et al., (1994), la eficacia superior de la heparina frente a la warfarina en la mayoría de los ensayos clínicos efectuados se debe a su mayor capacidad para prevenir la trombosis venosa aguda distal y no la trombosis proximal, la cual es mucho más relevante desde la perspectiva clínica.
|
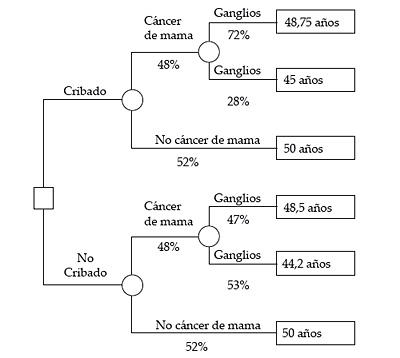
RECUADRO 5. Estimación de la efectividad del cribado de cáncer de mama familiar (Alonso, inv. principal, 2002). Introducción. El cáncer de mama es la neoplasia con mayor incidencia en la población femenina y la causa de muerte más habitual en mujeres de 35 a 65 años. En un 80-85 por 100 de los casos el cáncer de mama es esporádico, pero en un 10-15 por 100 de las ocasiones se identifican una serie de antecedentes familiares que conducen a considerar el cáncer de mama como «familiar». Se estima en la literatura médica que un 5-10 por 100 de los casos de cáncer de mama familiar obedecen a una predisposición hereditaria (mutaciones de los genes BRCA1 y BRCA2). Como la detección de mutaciones genéticas es un proceso laborioso, dado que en su gran mayoría las mutaciones son específicas de cada familia y muy heterogéneas, entretanto, debe evaluarse si se incluye o no a todas las personas con riesgo de ser portadoras en un programa de cribado y vigilancia. Objetivos. Estimar los efectos potenciales sobre la esperanza de vida de los pacientes de alto riesgo de dos estrategias alternativas: cribado de cáncer de mama familiar (exploración clínica y mamografía anual de los 30 a los 80 años) versus no cribado. Métodos. Los autores construyen un árbol de decisión (véase figura 3) para una hipotética mujer de Las probabilidades y resultados del árbol se estimaron del siguiente modo:
Resultados. En el Recuadro 1 vimos que la aplicación de la regla de la utilidad esperada servía para determinar la estrategia óptima. Dicha regla se basaba en la combinación lineal de probabilidades y utilidades. Pues bien, esa misma regla es de aplicación en casos como el de la figura 3, aun cuando no haya utilidades. Como la medida de los resultados se expresa en unidades cuantitativas (años de vida) podemos multiplicar cada resultado por su respectiva probabilidad a semejanza de lo que hacíamos para calcular la utilidad esperada, sólo que ahora la calificamos como regla del valor esperado. Figura 3. Árbol de decisión para la elección (
Si aplicamos dicha regla para resolver el árbol de decisión, obtenemos que la opción «cribado» produce una esperanza de vida de: 0,48 × [0,28 × 45 + 0,72 × 48,75] + 0,52 × 50 = 48,896 años mientras que la opción «no cribado» genera: 0,48 × [0,53 × 44,2 + 0,47 × 48,5] + 0,52 × 50 = 48,186 años En consecuencia, el cribado es una opción más efectiva que el no cribado, ya que incrementa la esperanza de vida en 0,71 años (8 meses y medio). |
Una vez asentado el concepto de medidas de efectividad en unidades físicas/clínicas, hay que reparar en las limitaciones que entraña su uso. La primera limitación, ya advertida, es que este tipo de medidas no siempre guardan una relación proporcional con las preferencias individuales. En parte, este problema de desafección de las preferencias puede paliarse si se utilizan medidas de resultados finales en lugar de medidas de resultados intermedios (por ejemplo, número de fracturas evitadas en lugar de porcentaje de aumento de la densidad de la masa ósea). No obstante, incluso en ese caso, podríamos encontrar situaciones en las que dos pacientes con características sociodemográficas y clínicas semejantes poseyeran actitudes o preferencias diferentes, de modo que las molestias y restricciones impuestas por una misma enfermedad no serían percibidas de la misma manera por uno que por otro.
Una segunda restricción proviene de la imposibilidad de comparar entre sí programas que dan lugar a resultados diferentes. Éste sería el caso de un tratamiento para la hipertensión y otro para la diabetes. Un problema similar se produce cuando se comparan programas cuya efectividad es multidimensional. Pensemos en el caso de un medicamento para infartados que reduce el riesgo se sufrir un nuevo infarto de miocardio pero que incrementa el riesgo de experimentar hemorragias gastrointestinales. La única forma de obviar los efectos adversos es asumiendo que «es más valioso prevenir un infarto que prevenir una hemorragia», lo cual no deja de ser un juicio de valor discutible.
Por último, este tipo de medidas participan de una limitación generalizable a las medidas de calidad de vida relacionada con la salud e incluso a los AVAC, concerniente a la dificultad para interpretar las ratios coste-efectividad. Como se verá en el epígrafe 5.1, tanto el ACE como el ACU emplean como criterio para tomar decisiones la ratio o razón coste-efectividad (coste-utilidad). Esta ratio es incremental, lo cual significa que compara el coste y la efectividad de la nueva tecnología que queremos evaluar con el coste y la efectividad del status quo o tecnología preexistente 11. Supongamos que la nueva tecnología es más coste-efectiva que la existente, de forma que produce 1 año extra de vida pero cuesta 60.000 euros adicionales. Ante este resultado, el gerente que deba efectuar una recomendación a la dirección del hospital se preguntará si realmente 1 año extra de vida «vale lo que cuesta», esto es, 60.000 euros más. Como la efectividad no se ha medido en las mismas unidades que los costes (euros) el incremento en efectividad no es directamente comparable con el incremento en costes, por lo que no puede concluirse si una tecnología sanitaria es coste-efectiva en términos absolutos. Por esta razón, las recomendaciones formuladas en los ACE suelen basarse en la comparación de la ratio obtenida con otras correspondientes a tecnologías más o menos dispares (tablas clasificatorias).
3.2. MEDIDAS DE CALIDAD DE VIDA RELACIONADA CON LA SALUD
La CVRS es un concepto multidimensional que idealmente abarcaría desde la función física –capacidad para ejercitar actividades físicas diarias, desplazamientos y cuidado personal– pasando por la psicológica –ansiedad, depresión, bienestar emocional– hasta incluir la percepción general de la propia salud.
Dos son los enfoques que se han seguido para intentar medir la CVRS, provenientes de tradiciones científicas diferentes: el enfoque psicométrico y el enfoque económico. Los dos enfoques tienen en común su fundamento en la percepción subjetiva del paciente. Ambos difieren, no obstante, en sus objetivos. Mientras que las medidas o escalas de CVRS del enfoque psicométrico pretenden reflejar el cambio en la salud experimentado por un paciente como efecto del tratamiento, o pretenden discriminar entre pacientes con diferentes niveles de gravedad, las medidas basadas en las preferencias del enfoque económico intentan medir la intensidad con que el paciente prefiere un estado de salud a otro. Estas medidas basadas en las preferencias son las que se combinan con la cantidad de vida para obtener los AVAC. Por esta razón, hay autores 12 que se refieren a las medidas de CVRS como medidas no basadas en las preferencias. En este apartado nos referiremos sólo a este tipo de medidas.
Los primeros intentos por medir la CVRS se remontan a la década de 1940 (Karnofsky y Burchenal, 1949), si bien no es hasta los años sesenta-setenta cuando podemos encontrar lo que hoy en día se concibe como medidas de CVRS, esto es, medidas caracterizadas por tres rasgos fundamentales (Badía y Lizán, 2003):
- La importancia de los dominios físico, psíquico y social en la multidimensionalidad del concepto.
- El carácter subjetivo de la medición, efectuada a partir de las respuestas de los pacientes a las preguntas o ítems en que se descompone cada una de las dimensiones de la CVRS.
- La conversión de las respuestas a los ítems en puntuaciones numéricas que se agregan para obtener una puntuación global para toda la escala de medición.
Las medidas de CVRS suelen juzgarse de acuerdo a una serie de criterios o propiedades psicométricas: viabilidad, fiabilidad, validez y sensibilidad al cambio.
El instrumento de medida de la CVRS será viable si puede administrarse sin incurrir en costes considerables, siendo necesario para ello que sea comprensible y rápido de completar. La escala de CVRS será fiable si da lugar a puntuaciones semejantes ante medidas repetidas en el mismo sujeto, ya sea en una misma encuesta (fiabilidad interna) o tras transcurrir un breve lapso de tiempo (fiabilidad test-retest). En cuanto a la validez, si bien existen varios tipos –aparente, de constructo, de criterio– en todos los casos se pretende determinar si el instrumento mide aquello que quiere medir. Por último, la sensibilidad al cambio es la capacidad de la escala para detectar cambios en la salud de los pacientes a consecuencia de la aplicación de un tratamiento.
En cuanto al tipo de medidas de CVRS que existen, es frecuente distinguir entre medidas específicas y medidas genéricas o perfiles de salud. Las primeras pretenden medir la CVRS asociada a pacientes afectados por una patología específica –asma, diabetes, depresión, etc.– de manera que aunque presumiblemente la sensibilidad al cambio de estas medidas será elevada, resultará difícil generalizar sus resultados a otros problemas de salud. Ejemplos de medidas específicas son Ashma Quality of Life Questionnaire, Skindex-29 o Diabetes Quality of Life Questionnaire.
Las medidas genéricas, en cambio, no se vinculan a una enfermedad concreta, de manera que son susceptibles de utilizarse con distintas poblaciones. Algunas de las medidas genéricas más importantes son Nottingham Health Profile, Short Form-36, o Sickness Impact Profile.
Ya sean medidas específicas o genéricas el procedimiento seguido para obtener el valor numérico representativo de la CVRS del paciente suele constar de tres fases:
- La respuesta a cada ítem recibe una puntuación. Por ejemplo, si nos fijamos en la figura 4 vemos que el primero de los dos ítems del SF-36 para medir la dimensión dolor corporal tiene seis respuestas posibles –«No, ninguno», «Sí, muy poco», «Sí, un poco», «Sí, moderado», «Sí, mucho», «Sí, muchísimo»– recibiendo la primera respuesta el valor uno, la segunda el valor dos…, así hasta la última que recibe el valor seis.
Figura 4. Ítems extraídos de la versión española del SF-36v2 Health Survey, adaptada por J. alonso y colabs.
|
7. ¿Tuvo dolor en alguna parte del cuerpo durante las 4 últimas semanas?
8. Durante las 4 últimas semanas, ¿hasta qué punto el dolor le ha dificultado su trabajo habitual incluido el trabajo fuera de casa y las tareas domésticas?
|
- Casi todas las medidas agregan las puntuaciones asignadas a los distintos ítems de una misma dimensión dando igual peso a cada uno de los ítems. Siguiendo con el mismo ejemplo anterior, si el paciente ha sentido dolor moderado durante las últimas cuatro semanas y dicho dolor ha llegado a dificultar mucho su trabajo fuera del hogar y tareas domésticas, entonces la puntuación de la dimensión dolor corporal sería 4 + 5 = 9. Dado que no todos los ítems tienen el mismo número de respuestas, es frecuente normalizar la anterior puntuación bruta de manera que la puntuación definitiva se exprese en una escala 0-100. Esto se consigue mediante la fórmula:
| Puntuación normalizada | = |
(Puntuación bruta - Puntuación mínima)
|
x | 100 | ||
|
(Puntuación máxima - Puntuación mínima)
|
Reemplazando los datos del ejemplo en esta fórmula, tendríamos que la puntuación normalizada sería igual a
|
(9 - 2)
|
x | 100 | = | 77,77 | ||
|
(11 - 2)
|
- Las puntuaciones correspondientes a cada una de las dimensiones que pretende medir la escala de CVRS se agregan para obtener una puntuación síntesis o resumen del conjunto de la CVRS del paciente. Sin embargo, este último paso sólo se da en unas pocas medidas de CVRS (por ejemplo, Sikness Impact Profile).
La descripción del proceso seguido para obtener las puntuaciones de las medidas de CVRS revela la principal limitación que ofrece este tipo de instrumentos para su utilización en la evaluación económica, a saber: la naturaleza arbitraria de los supuestos que subyacen a cada una de las fases de agregación.
El primero de los pasos que hemos visto asume implícitamente que un paciente asigna el mismo peso a cada uno de los intervalos comprendidos entre dos respuestas consecutivas a un ítem. Por ejemplo, el SF-36 supone (ítem 8 de la figura 4) que el paciente pondera del mismo modo el intervalo comprendido entre «Nada» y «Un poco» que el intervalo que media entre «Bastante» y «Mucho». Este supuesto dista mucho de ser auto-evidente, ya que dependerá de cuál sea la intensidad de preferencias del paciente.
Para poder asumir que el intervalo 2-1 del segundo de los ítems de la dimensión dolor corporal del SF-36 es equivalente al intervalo 5-4 la escala de medida de las respuestas a ese ítem debería ser una escala intervalo, y no meramente una escala ordinal. Una escala ordinal posee la propiedad de que el orden entre dos mediciones cualesquiera permanece invariable ante cualquier transformación monótona 13. Si una puntuación de 40 designa una CVRS mejor que la que corresponde a una puntuación de 20, entonces una puntuación de 40 × 2 = 80 seguirá siendo preferida a una puntuación de 20 × 2 = 40, ya que multiplicar por 2 las puntuaciones originales es una transformación monótona. Sin embargo, esta propiedad no es suficiente para el tipo de comparaciones que efectúa la evaluación económica. Necesitamos un tipo de escala cardinal conocida como escala intervalo, la cual garantiza que razones incrementales como las que se utilizan en el ACE para determinar qué tecnología sanitaria es preferible permanecerán invariables ante cualquier transformación afín positiva 14.
|
RECUADRO 6. Escalas de CVRS, transformaciones monótonas y transformaciones afines positivas. Supongamos que tenemos dos tecnologías A y B mutuamente excluyentes (por ejemplo, dos variedades de un mismo medicamento). La tecnología A tiene una efectividad medida en una escala de CVRS de 5, mientras que la tecnología B la tiene de 4. Supongamos también que la efectividad del programa que viene financiándose por defecto –el status quo– es de 2. Supongamos finalmente que la tecnología A cuesta 2,65 unidades monetarias, la B cuesta 2 unidades, y el status quo cuesta 1 unidad. Como la finalidad de la evaluación es determinar cuál de las dos tecnologías rivales debería reemplazar a la tecnología vigente, los costes y efectividades de las nuevas tecnologías deberían compararse con el coste y la efectividad del status quo. La efectividad adicional que proporciona la tecnología A respecto del status quo es de 5 – 2 = 3, mientras que la efectividad extra de la tecnología B es de 4 – 2 = 2. Así pues, el cociente relativo de efectividades es de 3/2 = 1,5. A su vez el cociente relativo de costes es (2,65 – 1) / (2 – 1) = 1,65. Por tanto, parece que la mayor efectividad de la tecnología A no compensa su mayor coste, de manera que no sería preferible a la tecnología B. Sin embargo, como la escala en la que hemos medido la CVRS admite cualquier transformación monótona, supongamos ahora que las puntuaciones se hubieran tomado en una escala que fuera el cuadrado de la anterior. Esto significaría que la nueva ratio de efectividades es 1,75 mientras que el cociente de costes continúa siendo de 1,65. Esto sugiere que la tecnología A es ahora preferible a la B. La única forma de evitar que la razón de los intervalos varíe arbitrariamente es utilizar escalas intervalo. Supongamos que las dos escalas de nuestro ejemplo lo fueran, de manera que las puntuaciones de la segunda escala se obtienen mediante la transformación 2 × E + 10, donde E representa la puntuación de efectividad de la primera escala. Puede comprobarse que ahora la razón de efectividades no varía, de forma que la tecnología A sigue sin ser preferible a la tecnología B. |
La misma crítica acerca de la arbitrariedad de las ponderaciones que implícitamente se atribuyen a los intervalos, se puede extender a la suma de las puntuaciones de los diferentes ítems que integran una dimensión. Por ejemplo, al sumar las puntuaciones de los ítems correspondientes a la función física del SF-36, estamos suponiendo que es igual de importante para el paciente poseer limitaciones para llevar la bolsa de la compra que para caminar 100 metros.
Por último, como la escala en que se miden las diferentes dimensiones no es común, en principio no pueden compararse dimensiones distintas entre sí. La combinación de las puntuaciones de cada dimensión mediante su suma simple no deja de ser nuevamente un procedimiento arbitrario.
|
RECUADRO 7. Medida de la CVRS en pacientes con incontinencia urinaria (García-Giralda y colabs, 2004). Introducción. La incontinencia urinaria es un problema de salud consistente en la pérdida involuntaria de orina, que constituye un problema social para la persona que lo sufre, afectando negativamente a su calidad de vida. Datos que evidencian las limitaciones que impone este problema sobre la CVRS es que un 60 por 100 de los pacientes afectados se sienten avergonzados de sus síntomas, un 60 por 100 de las mujeres afectadas evitan alejarse de sus hogares, un 45 por 100 no utiliza el transporte público y un 50 por 100 rechaza la actividad sexual. Objetivos. El objetivo principal del estudio fue la evaluación de la CVRS de los pacientes con incontinencia urinaria tratados en atención primaria. Métodos. El diseño del estudio fue longitudinal, no controlado, con mediciones de la CVRS de 52 pacientes antes y después de haberles puesto tratamiento. La CVRS fue valorada mediante una medida específica –cuestionario I-QoL sobre incontinencia– y una medida genérica –SF-12–. Resultados. La puntuación media del SF-12 al comienzo del estudio fue de 34,17, situándose al final del tratamiento en 39,25, habiéndose producido una mejora relativa del 14,87 por 100 (significativa al 99%). El resultado alcanzado con el cuestionario I-QoL fue similar, pasando el valor medio de 42,31 al inicio del estudio a 52,54 a su conclusión, experimentando una mejora relativa del 24,18 por 100 (también significativa al 99%). |
3.3. LOS AÑOS DE VIDA AJUSTADOS POR LA CALIDAD
3.3.1. Definición de los años de vida ajustados por la Calidad y metodología de cálculo
Los AVAC pueden definirse como un índice que combina en un solo número la cantidad de vida con la CVRS. En concreto, para ser más precisos, los AVAC son el producto de dos factores: los años de vida y la utilidad o bienestar asociado a la CVRS en la que se va a vivir durante esos años. Esta combinación la podemos representar de forma muy simple:
AVAC = U(Q, T) = V(Q) × T
donde T simboliza los años de vida, Q la calidad de vida, y V(Q) es la utilidad –también llamada peso de calidad (quality weight)– que extrae el individuo de vivir en Q.
La anterior formulación puede extenderse a situaciones en las que el estado de salud no permanece constante –como suele ser normal durante el proceso de recuperación tras un accidente– sumando simplemente tantos productos V(Q) × T como variaciones experimente la CVRS. Imaginemos una convalecencia de tres meses en el hospital, seguida por un periodo de recuperación en el hogar de otros tres meses, tras lo cual se restablece la salud normal del paciente durante un plazo de cinco años y medio, al término de los cuales muere. El número de AVAC correspondiente a este perfil de salud no permanente se calcularía (en años) como
0,25 × V(convalecencia) + 0,25 × V(recuperación) + 5,5 × V(salud normal) + V(muerte)
Los AVAC presentan dos ventajas notables respecto de las medidas de CVRS que estudiamos en el epígrafe anterior:
- Superan las limitaciones de que adolecían aquéllas, ya que los AVAC sí son medidas basadas en las preferencias, puesto que las V(Q) lo son. Es más, son medidas cardinales de preferencias, ya que las técnicas de medición que se emplean para estimar la utilidad V(Q) poseen propiedades de escala intervalo. Los dos puntos que se adoptan como anclas para definir la escala intervalo son la salud normal a un extremo y la muerte al otro, asignándoseles convencionalmente los valores 1 y 0, respectivamente. Con los datos del ejemplo anterior, si las utilidades se han medido en una escala 0-1, donde V(muerte) = 0 y V(salud normal) = 1, y las preferencias son tales que V(convalecencia hospital) = 0,7 y V(recuperación hogar) = 0,8, el número total de AVAC sería de 5,875.
- Combinan cantidad y calidad de vida, ofreciendo posibilidades fuera del alcance de las escalas psicométricas de CVRS, ya que permite comparar tratamientos que sólo proporcionan supervivencia con tratamientos que sólo mejoran la calidad de vida.
Los primeros intentos por construir indicadores semejantes a los AVAC se remontan a los años setenta 15, si bien fueron Pliskin et al., (1980) quienes primero caracterizaron sus propiedades teóricas, formulando las condiciones que deben satisfacer las preferencias individuales para ser descritas correctamente por los AVAC (validez empírica o descriptiva).
Tres son las condiciones o supuestos que deben obedecer las preferencias para que las mediciones en AVAC sean válidas empíricamente 16:
- La preferencia por ganar años de vida debe ser independiente de la preferencia por ganar calidad de vida, y viceversa. Este supuesto es el que permite calcular los AVAC como el producto de dos factores.
- La preferencia por ganar años de vida debe ser neutral al riesgo. Este supuesto requiere que el individuo sea indiferente entre un tratamiento incierto y un tratamiento seguro, produciendo ambos el mismo número esperado de años.
- La preferencia por sacrificar años de vida a cambio de ganar calidad de vida debe ser una proporción constante del número total de años. Por ejemplo, si se está dispuesto a renunciar a un año de los 10 en que se puede vivir en un estado intermedio a cambio de recuperar la salud normal, entonces se debería estar dispuesto a renunciar a 1/2 año de cinco (la proporción 0,1 = 1/10 = 0,5/5 debe mantenerse constante).
Para calcular la ganancia en AVAC que reporta un nuevo programa sanitario se requiere seguir tres pasos:
- Obtener la utilidad de la CVRS.
- Multiplicar dicha utilidad por los años de vida.
- Hallar la diferencia entre los AVAC aportados por el nuevo programa y los AVAC aportados por el status quo.
De los tres pasos formulados el primero de ellos es el crucial, ya que requiere la medición de las preferencias. Si la perspectiva de la evaluación es la perspectiva social, entonces las preferencias deberán provenir de la sociedad en general y no de colectivos específicos. Por su parte, los datos relativos a tiempo de vida provienen de las fuentes clínicas ya comentadas al describir las medidas de efectividad en unidades físicas/clínicas. El último de los pasos no es más que la comparación de los AVAC previamente calculados.
3.3.2. Obtención de los valores de utilidad (preferencias)
Dos son las maneras de obtener las utilidades de la CVRS: la primera consiste en medir directamente las preferencias con técnicas diseñadas al efecto; la segunda pasa por obtenerlas indirectamente por medio del algoritmo de cálculo generado por alguno de los llamados sistemas multiatributo.
Dentro de las medidas directas de preferencias, las predilectas por parte de los evaluadores económicos son aquellas basadas en elecciones, como es el caso de la lotería estándar (standard gamble) o el intercambio temporal (time tradeoff). Un tercer método no basado en elecciones es la escala visual analógica (visual analogue scale), si bien existe un amplio consenso acerca de su menor validez, razón por la cual no vamos a describirla aquí 17.
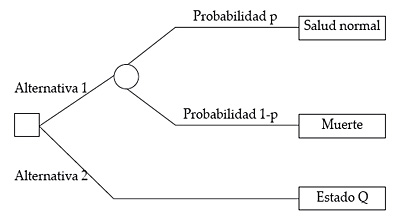
La lotería estándar compara dos alternativas (figura 5). La alternativa 1 es un tratamiento con dos posibles resultados: o el paciente recobra su salud normal y vive durante t años más (probabilidad p) o bien muere (probabilidad 1-p). La alternativa 2 ofrece con certeza la seguridad de vivir en el estado de salud crónico Q durante t años. Se varía la probabilidad p hasta que el entrevistado es indiferente entre ambas alternativas, fijándose la utilidad de Q igual a p.
Figura 5. Lotería estándar
El intercambio temporal también plantea una elección entre dos alternativas (figura 6). La alternativa 1 representa permanecer en el estado de salud Q durante t años, tras los cuales fallece, mientras que la alternativa 2 ofrece vivir × años (× < t) con salud normal. La duración × se va variando hasta que el individuo se muestra indiferente entre las dos alternativas, fijándose la utilidad de Q igual al cociente ×/t.
Figura 6. Intercambio temporal
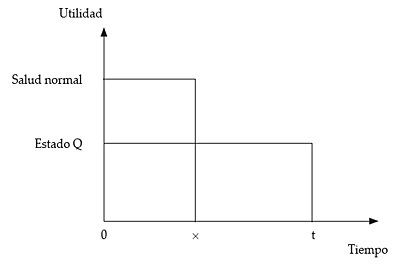
Si bien durante años se ha venido predicando la superioridad de la lotería estándar frente al intercambio temporal, dado que encuentra su fundamento en la teoría de la utilidad esperada (véase el primer epígrafe del capítulo), en la actualidad se dispone de alguna evidencia que sugiere que las mediciones del intercambio temporal podrían tener menos sesgos. En cualquier caso, es una cuestión sobre la que no existe consenso.
En el siguiente recuadro se ilustra la medición de las preferencias mediante el método que acabamos de ver (intercambio temporal), al tiempo que permite verificar cómo la intuición clave que subyace a los AVAC –cantidad de vida bruta ajustada por la calidad– puede adaptarse a las especificidades de diferentes contextos clínicos, como es el caso de la oncología, produciendo una medida sui generis.
|
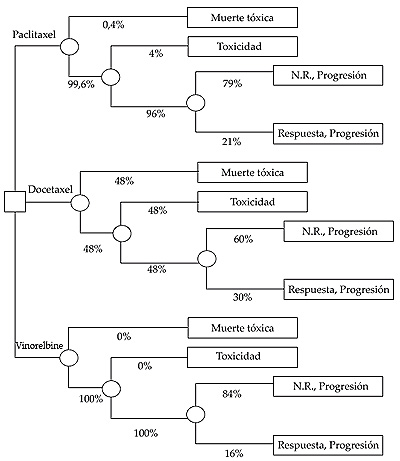
RECUADRO 8. Una estimación de la supervivencia ajustada por la calidad en quimioterapia (leung et al., 1999). Introducción. Los medicamentos antitumorales conocidos como antraciclinas están considerados como los principales agentes para paliar los efectos del cáncer de mama metastásico. Sin embargo, con el tiempo, casi todos los pacientes tratados desarrollan resistencia al efecto de estos fármacos. Esto es un grave problema, ya que la supervivencia mediana tras haberse vuelto el cáncer de mama resistente a las antraciclinas es inferior a un año. No obstante, hay tres nuevos medicamentos –paclitaxel, docetaxel y vinorelbine– que pueden aplicarse a pacientes resistentes a las antraciclinas, desconociéndose cuál de los tres es el más efectivo. Figura 7. Árbol de decisión para la elección (
Objetivos. Determinar cuál de los tres fármacos es más coste-efectivo según un ACU. Métodos. Se confeccionó un árbol de decisión (figura 7) en el que representar las consecuencias de los tres medicamentos. Los datos relativos a las probabilidades y tiempo de supervivencia hasta que vuelve a progresar el cáncer se extrajeron de tres ensayos clínicos publicados. Las utilidades se obtuvieron por medio del método del intercambio temporal. Para ello se entrevistó a 25 voluntarias sanas y a 25 enfermas de cáncer, a las que se les preguntaba por el tiempo en buena salud que consideraban equivalente a pasar cuatro meses (tiempo medio de duración del tratamiento) en cada uno de los resultados representados en el árbol. Así, por ejemplo, si la entrevistada contestaba que consideraba equivalente 1 mes en buena salud a cuatro meses sin obtener respuesta del tratamiento, la utilidad del resultado «No respuesta» se fijaba en 1/4 = 0,25. Finalmente, las utilidades medias de cada resultado se multiplicaban por el tiempo medio de supervivencia antes de la progresión de la enfermedad para obtener los Días de Vida Libres de Progresión Ajustados por la Calidad. Resultados. Utilizando las utilidades de los voluntarios, el vinorelbine fue el medicamento que ofrecía una mayor supervivencia ajustada por la calidad (38 días frente a 33,6 y 37,2 días el docetaxel y el paclitaxel, respectivamente). En cambio, el paclitaxel fue el tratamiento más efectivo cuando se emplearon las utilidades de los pacientes (39,8 días frente a 33,2 y 35 días el docetaxel y el vinorelbine, respectivamente). Esta discrepancia nos muestra cómo diferentes perspectivas (social vs del paciente) pueden conducir a resultados distintos, ya que no es lo mismo juzgar un estado de salud ex ante que ex post. |
La segunda de las formas de medición de las preferencias (sistemas multiatributo) es menos costosa que la medición directa, si bien se expone al riesgo de que los valores generados no representen adecuadamente las preferencias de la población objetivo del análisis. Entre los sistemas multiatributo más importantes cabe incluir Quality of Well- Being, Health Utility Index y EuroQol-5D.
Estos sistemas poseen dos componentes: un sistema de clasificación de estados de salud multidimensionales y un algoritmo que asocia un valor a cada uno de los estados generados. Por ejemplo, el sistema EuroQol-5D es capaz de generar hasta 243 estados diferentes, cada uno de ellos caracterizado por cinco dimensiones. A partir de estimaciones directas efectuadas con una muestra representativa de la población general se estimó el algoritmo que asigna un valor a cada estado. Así, al estado 11223 del EuroQol 18 se le asigna el valor 0,255.
3.3.3. Críticas y limitaciones de los años de vida ajustados por la Calidad
Probablemente, la objeción más importante que se realiza a los AVAC radique en las dudas existentes respecto a la validez de sus supuestos. Por ejemplo, como ya sabemos, el hecho de que los AVAC se calculen como el producto de T y V(Q) implica que se está suponiendo que la preferencia por el tiempo de vida es independiente de la preferencia por la calidad de vida, y viceversa. Este supuesto es contradictorio con preferencias como las que pueden producirse con pacientes con problemas de salud muy limitativos (por ejemplo, encamados), en las que a partir de un cierto periodo de tiempo ya no toleran vivir así 19. En casos como éstos los AVAC no describirán de forma válida las preferencias individuales. Otro tipo de críticas provienen de la ausencia de las consideraciones de justicia distributiva al agregar los AVAC de la población. A este respecto, suele afirmarse que «1 AVAC vale 1 AVAC, no importa a quien corresponda». Hay que precisar, no obstante, que como ya se expuso al describir los fundamentos normativos de la evaluación económica (epígrafe 1.1), nada impide introducir la dimensión equidad en el ACU. Por último, la mayor limitación de los AVAC es análoga a la que ya describimos al tratar las medidas de efectividad: en principio no sabemos cuánto «vale» 1 AVAC, de manera que ignoramos si la ganancia en AVAC compensa o no el mayor coste en que se incurre.
3.4. LA VALORACIÓN MONETARIA DE LOS RESULTADOS DE SALUD
El gran potencial del ACB proviene de la valoración de costes y beneficios en una unidad común: el dinero. El rechazo que tradicionalmente ha suscitado la monetización explícita de los resultados de salud en el ámbito sanitario, obedece a una incorrecta comprensión de la finalidad de la evaluación económica. No se trata de poner precio a la vida humana, sino de ser consecuente con el hecho de que preservar la vida humana tiene un coste de oportunidad, y al valorar los beneficios en unidades monetarias podemos conocer si el programa o tecnología en evaluación vale lo que cuesta.
Tres son las direcciones que ha seguido el trabajo empírico dedicado a la valoración monetaria de los resultados de salud:
- El enfoque del capital humano.
- El enfoque de las preferencias reveladas.
- El enfoque de las preferencias declaradas.
En los años sesenta y setenta llegó a ser popular la cuantificación monetaria de los beneficios de salud, caracterizados en términos de rendimientos derivados de la inversión en capital humano que representa seguir un tratamiento. El enfoque del capital humano supone que el individuo invierte en su propia salud a fin de ser más productivo, y que esa mayor productividad se reflejará en unos mayores ingresos futuros. Por tanto, podemos valorar los beneficios de los tratamientos atendiendo a los ingresos monetarios que el individuo percibiría al ampliarse el tiempo que puede estar trabajando.
Sin embargo, desde muy pronto arreciaron las críticas a la utilización de este enfoque como método exclusivo para valorar monetariamente los resultados de salud. En concreto, Mishan (1971) formula dos críticas ampliamente aceptadas:
- El enfoque del capital humano se asienta en el cuestionable supuesto de que el principal objetivo social es maximizar la renta nacional, lo cual significaría no financiar programas que mejoran la salud de personas con ingresos futuros reducidos o nulos.
- El enfoque del capital humano es inconsistente con los fundamentos normativos del ACB, que ya vimos en el epígrafe 1.1 que se basan en el criterio de compensación o mejora potencial de Pareto.
El enfoque de las preferencias reveladas recibe ese nombre por el hecho de inferir las valoraciones monetarias de los resultados de salud de las decisiones que toman los agentes en los mercados. La inexistencia de un mercado sanitario que señalice vía precios el valor de los programas sanitarios, obliga a observar otros mercados como el laboral donde los salarios pueden revelar de forma implícita o indirecta dicho valor. Por ejemplo, el denominado método de los salarios hedónicos estima el valor monetario de una vida humana o de un problema de salud a partir de la observación del intercambio o transacción que efectúan los trabajadores entre riesgo y salario. Si se estima que las personas piden en promedio 600 euros más al año como compensación por desempeñar un empleo que aumenta en un 1 por 100 el riesgo anual de sufrir un accidente mortal, entonces el valor monetario de una vida se cifra en 60.000 euros ( = 600/0,01).
Otros métodos de preferencias reveladas basados también en la observación de transacciones en mercados de bienes relacionados, serían el método de la función de producción de salud o el método del coste del viaje 20.
La gran ventaja de todos estos métodos es que se fundamentan en las preferencias que revelan los sujetos en sus decisiones de mercado. Poseen no obstante flancos débiles, los cuales les restan utilidad para orientar la toma de decisiones en el sector sanitario. Primero, nos encontramos con el problema de que habrá dimensiones de la calidad de vida relacionada con la salud –la ansiedad, por ejemplo– que no serán objeto de valoración. Además, todas aquellas preferencias que no sean estrictamente individuales (esto es, las preferencias altruistas) no serán valoradas. Finalmente, por definición, el enfoque de las preferencias reveladas no permite la estimación de costes y beneficios de los programas sanitarios antes de su aplicación. La única perspectiva de análisis posible es la ex post.
Llegamos así al enfoque más fértil en el terreno de la evaluación económica de la asistencia sanitaria, el enfoque de las preferencias declaradas. Reciben este nombre un conjunto de métodos caracterizados por recabar las preferencias de la población de forma directa, mediante la utilización de cuestionarios. Existen dos tipos de métodos directos: el método de la valoración contingente y los métodos multiatributo.
El método de la valoración contingente recrea un mercado virtual mediante una encuesta donde el papel de la oferta es representada por el encuestador, la demanda por el encuestado y el precio de mercado por la máxima cantidad de dinero que está dispuesto a pagar el encuestado –su disposición a pagar (DAP)– por una mejora en la salud o por una reducción en el riesgo de enfermar. Se dice que la valoración del bien es contingente al mercado simulado. De ahí el término utilizado para denominar a este método.
De modo alternativo a la DAP, podría preguntarse al encuestado por la mínima suma de dinero que estaría dispuesto a aceptar –su disposición a aceptar (DAA)– como compensación por no beneficiarse del programa sanitario. En teoría la DAA declarada por el individuo debería ser idéntica a su DAP 21.
Existen varios autores (por ejemplo, O`Brien y Gafni, 1996) que han intentado establecer cuáles son las cuestiones clave que debe tener presente cualquier estudio de valoración contingente para valorar correctamente los resultados de salud de un programa sanitario. Por ejemplo, ¿qué tipo de medida utilizar? ¿DAP o DAA? Pinto y Sánchez (2003) resumen en ocho los pasos que debe seguir un ejercicio de valoración contingente para intentar abordar con éxito cuestiones como la recién planteada:
- Definición del producto.
- Perspectiva de la valoración.
- Definición del modo de pago.
- Elección del tipo de pregunta.
- Elección del contexto social.
- Forma de administración de las encuestas.
- Elección de la población relevante.
- Agregación de las preferencias.
El siguiente recuadro ilustra la aplicación de estos pasos por medio de un estudio real.
|
RECUADRO 9. Disposición a pagar por reducciones en los ataques de angina de pecho (Kartman et al., 1996). Introducción. La angina de pecho suele deberse a episodios de isquemia miocárdica (desequilibrio entre la demanda de energía del corazón y la oferta de oxígeno). La frecuencia con que se padecen los ataques de angina de pecho suele utilizarse como una medida clínica de la gravedad de la isquemia. En este estudio se aplica el método de la valoración contingente para estimar en unidades monetarias la ganancia en salud que representa una reducción en la frecuencia de ataques de angina de pecho. Objetivos. Este trabajo persigue dos objetivos: 1. Contrastar la validez interna de la valoración contingente como método para valorar la DAP por reducciones en la frecuencia de ataques de angina de pecho; 2. Comparar si las DAP medias obtenidas por dos formatos distintos de preguntas son coincidentes o no. Métodos. En primer lugar, el producto a valorar fue la reducción en el riesgo de sufrir un ataque de angina de pecho. La población del estudio fueron 402 enfermos de angina de pecho. En consecuencia, la perspectiva del estudio fue ex post ya que los entrevistados habían experimentado previamente la enfermedad. éstos fueron agrupados aleatoriamente en tres submuestras que se diferenciaban en el porcentaje de reducción en el número de ataques de angina semanales –25%, 50%, 75%– que conseguía un nuevo medicamento, que se presentaba como más efectivo que el que estaban tomando los pacientes (contexto social). A su vez, cada participante en el estudio fue asignado aleatoriamente a una de las siguientes sumas de dinero (en coronas suecas; 1$ = 7,251 coronas): 120, 240, 360, 500, 1.000, 2.000, 5.000, 10.000. La forma de administración de las encuestas fue telefónica. Se utilizaron dos tipos de pregunta diferentes para estimar la DAP: el formato binario y el formato de la subasta (bidding). A cada uno de los entrevistados se les preguntaba si estarían dispuestos a pagar la suma a la que habían sido aleatoriamente asignados (por ejemplo, 360 coronas), a lo cual tenían que contestar sí o no (formato binario). Dependiendo de la respuesta la suma era incrementada o reducida utilizando las otras cantidades (subasta), hasta que la respuesta inicial era cambiada (por ejemplo, de «sí» pasaba a «no»). Se insistió a los encuestados en que la suma en cuestión debería ser pagada de modo adicional al copago habitual y que dicha cantidad adicional provendría de los ingresos del encuestado (modo de pago). La DAP mediante el formato de subasta se estimaba como el punto medio del intervalo acotado por una respuesta «sí» y una respuesta «no» (por ejemplo, 750 coronas para una persona que contestase «sí» a un precio de 500 coronas y contestase «no» a un precio de 1.000 coronas). A partir de las DAP individuales así calculadas se estimaba la DAP media. Con los datos binarios la DAP media se estimó con un análisis de regresión logística. Se utilizaron dos especificaciones, una lineal y otra log-lineal. Resultados. El primer resultado de interés es que las DAP medias (forma de agregación de las preferencias) obtenidas por medio de los dos formatos de preguntas fueron semejantes. Las cantidades estimadas para la especificación log-lineal con datos binarios fueron 1.540, 2.542 y 2.900 coronas para reducciones del 25 por 100, 50 por 100 y 75 por 100, respectivamente. Las cantidades correspondientes estimadas con los datos de subasta ascendieron a 1.388, 2.079 y 3.350 coronas. En segundo lugar, parece poder afirmarse que el ejercicio de valoración contingente realizado es válido internamente. Esta conclusión se basa en cuatro resultados alcanzados: 1. La DAP aumentaba con el nivel de renta de los participantes; 2. La DAP era tanto mayor conforme lo era la tasa de ataques de angina de partida; 3. La DAP era tanto mayor cuanto mayor era la reducción en la frecuencia de ataques; 4. La DAP era tanto mayor cuanto más grave era el estado de salud del entrevistado (angina de pecho estable o inestable). Finalmente, se constató la presencia del que es considerado el principal sesgo del formato de subasta –sesgo del punto de partida (starting-point bias)– de forma que la DAP media de los pacientes asignados al punto de partida más pequeño (120 coronas) fue de 2.025 coronas mientras que dicha DAP ascendió a 4.000 coronas para aquellos pacientes asignados a la cantidad más alta (10.000 coronas). |
Las principales desventajas de la valoración contingente tienen que ver con los sesgos que suelen afectar a sus estimaciones, y que se derivan del carácter hipotético de las respuestas. Por ejemplo, es frecuente encontrar el llamado efecto incrustación que describe el fenómeno consistente en que la DAP suele ser insensible a la magnitud del bien objeto de evaluación. En este sentido, el ejemplo del recuadro anterior representa una excepción, ya que hemos visto que en ese estudio la DAP variaba cuando lo hacía la frecuencia de ataques de angina de pecho. Adicionalmente, la valoración contingente presenta dificultades añadidas en el contexto específico de la salud, ya que la monetización explícita de un bien superior como es la salud puede suscitar el rechazo de los encuestados.
En parte como respuesta a los problemas que rodean a la valoración contingente, en parte con la pretensión de enriquecer la evaluación económica de los programas sanitarios, valorando no sólo los resultados de salud sino también los medios para obtener dichos resultados, se han postulado los métodos de preferencias declaradas multiatributo. Como su propio nombre sugiere, estos métodos se basan en la descripción de un bien por medio de los atributos o dimensiones que lo caracterizan. Por ejemplo, de acuerdo a estos métodos un medicamento podría describirse como una combinación de atributos como dosis, efectividad, efectos adversos y precio. El entrevistado tiene que ordenar, puntuar o elegir entre varias alternativas definidas de forma multiatributo. Esta técnica recibe el nombre de análisis conjunto (conjoint analysis) o, en términos más generales, experimentos de elección discreta (discrete choice).
El análisis conjunto permite identificar las relaciones de intercambio que existen entre atributos de proceso y atributos de resultado. Un atributo de proceso es, por ejemplo, el tiempo de espera hasta que el paciente es operado, mientras que uno de resultado es la ganancia en esperanza de vida. Los métodos multiatributo permiten conocer la tasa a la que el paciente está dispuesto a sacrificar tiempo de vida por menor tiempo de espera. Si el precio del tratamiento se incluye como un atributo más, entonces puede estimarse el valor monetario o DAP por cualquiera de los atributos. El siguiente recuadro ilustra la aplicación del análisis conjunto al caso de los servicios de ortodoncia.
|
RECUADRO 10. ¿Cómo proveer los servicios de ortodoncia? (Ryan y Farrar, 2000). Objetivos. El artículo ilustra la utilidad del análisis conjunto, analizando las relaciones de intercambio que establecen los sujetos entre localización de los servicios y tiempo de espera. Métodos. Se entrevistó a 160 pacientes de tres clínicas en Escocia. Los atributos y sus niveles fueron los recogidos en la tabla 3. Hay 16 escenarios posibles. En total se presentaron 15 elecciones a cada entrevistado, pidiéndosele en cada caso que señalase cuál de dos opciones prefería. A partir de las respuestas de los encuestados se procedió a estimar mediante un análisis de regresión los coeficientes de la siguiente ecuación: ∆B = β1 ∆LOC1 + β1 ∆LOC2 + β3 ∆ESPERA donde ∆B es el cambio en el bienestar que experimenta un paciente al tener que pasar del status quo a una alternativa, y las variables explicativas son las diferencias entre los niveles de los atributos tal y como fueron definidos en la tabla 3. Los coeficientes β nos indican la importancia relativa de cada uno de los atributos. Por ejemplo, β1 muestra el cambio en el bienestar que ocasiona pasar de ser atendido en primera consulta en el hospital a ser atendido en una clínica local. Tabla 3. Atributos y niveles incluidos en el estudio
Resultados. Los resultados mostrados en la tabla 4 revelan que hay una ganancia de bienestar al pasar de ser atendido en el hospital a serlo en una clínica (signo positivo de los coeficientes β1 y β2), mientras que el aumento en el tiempo de espera deteriora el bienestar (signo negativo de β3). Si utilizamos los valores de los coeficientes para examinar las transacciones entre atributos, podemos constatar que los individuos están dispuestos a esperar 1,3 meses extra ( = 0,77/0,59) a cambio de poder ser atendidos en su primera cita en una clínica y 1,5 meses extra ( = 0,91/0,57) para ser atendidos en segunda y demás citas. Tabla 4. Resultados del análisis de regresión
|
10 Esta distinción es paralela a la que con anterioridad se mencionó en relación con la medida del consumo de recursos requerido para administrar los tratamientos y su coste.
11 El status quo puede consistir en la mejor práctica disponible, una combinación de varias o incluso en la opción «No hacer nada».
12 Véase Brazier et al., (1999) para tener una panorámica exhaustiva sobre el tema.
13 Si X e Y son dos escalas cuyas unidades son números reales, diremos que Y es una transformación monótona de X si genera mayores (menores) valores cuanto mayores (menores) son los valores generados por X.
14 Si X e Y son dos escalas cuyas unidades son números reales, diremos que Y es una transformación afín positiva de X si Y = a + b X, donde b > 0.
15 El lector interesado en conocer la genealogía de los AVAC es remitido a Drummond et al., (2005).
16 Habría una cuarta condición que debería cumplirse en caso de querer calcular los AVAC correspondientes a un perfil de salud no permanente (Abellán y Pinto, 2000): la preferencia por cada par (Q, T) debe ser independiente del resto del perfil. Este supuesto es el que permite calcular el número de AVAC del perfil como una suma.
17 Una excelente revisión de las potencialidades y limitaciones de la escala visual analógica puede encontrarse en Torrance et al., (2001).
18 El código 11223 corresponde con: ningún problema para moverse, ningún problema para realizar las labores de cuidado personal, algunos problemas para realizar actividades cotidianas, algún dolor/malestar, mucha ansiedad/depresión. Una explicación detallada del sistema EuroQol-5D puede encontrarse en Badía et al., (1999).
19 Este fenómeno, observado empíricamente en varios estudios, se conoce como tiempo máximo tolerable (maximum endurable time) y fue descrito por vez primera por Sutherland et al., (1982).
20 Estos y otros métodos de preferencias reveladas se describen en detalle en Pinto et al., (2003).
21 La DAP y la DAA serían la medición empírica de dos conceptos teóricos conocidos en la Economía del Bienestar con los nombres de variación compensatoria y variación equivalente, respectivamente.